Neuroscience

Visual perception of coordinated rhythmic movements

Other coordination posts are here.

Fontaine et al (1997) and Wenderoth et al (2002) had empirically established that a key prediction of the dynamic pattern hypothesis was false: learning was easier closer to 0° than it was to 180°. The HKB attractor layout did not appear to be pulling behaviour in the expected manner; what was going on?

However, recently some evidence was provided that movement perception may play an important role by stabilizing rhythmical coordination patterns (Mechsner, Kerzel, Knoblich, & Prinz, 2001). Additionally, it was shown that the visual perception of phase relations close to 0º is more stable than that close to 180º (Zaal, Bingham, Schmidt, & Richard, 2000). Therefore, an alternative explanation would be that the Φ = 180º pattern is perhaps not just produced but particularly perceived less accurately than the Φ = 0º pattern. From this perspective, our data may reflect participants’ inability to discriminate between the Φ = 180º pattern and a pattern that is just 36 or 60º away. By contrast, the Φ = 0º pattern may represent a more accurately perceived pattern, such that a drift towards this attractor can be voluntarily avoided.
Wenderoth, Bock & Krohn, 2002

This brief comment at the end of their paper was a reference to the work from Geoff Bingham's lab on the visual perception of relative phase, which began with Bingham et al (1999) and was followed up in Zaal et al (2000) and Bingham et al (2001). Bingham et al noted that the HKB function is organised with respect to relative phase (Φ), and that participants were able to follow the instruction to produce, at least, 0º and 180º. This implies that people are able to control relative phase, and this entails that people must be able to perceive relative phase - you cannot control what you cannot perceive. In addition, Schmidt et al (1990) had shown that the HKB function persists when the coordination is occurring between people, with the participants watching each other. Bingham et al therefore investigated the visual perception of relative phase.

Participants viewed displays of two dots oscillating at some mean relative phase, with some level of variability in that mean (phase variability). The dots moved according to either human kinematics recorded from Schmidt et al or according to a sine function with noise. These two dots oscillated either in depth or from side to side; participants were either asked to judge mean relative phase or phase variability. Zaal et al (2000) tidied the methodology, and Bingham et al (2001) extended the results to include a careful manipulation of frequency - recall that as frequency increases, 180º becomes unstable and 0º, while remaining relatively stable becomes noisier.

The results were striking:

Judgments of Mean Phase

Mean relative phase was well perceived on average; judgments of mean relative phase on a scale of 1 (0º) to 180º (10) varied linearly with actual mean relative phase (Figure 1A);
However, the within-subject standard deviation of these judgments varied as an asymmetric inverted-U shaped function of mean relative phase (see Figure 1B). Judgments were stable at 0º, stable but less so at 180º, and they became more and more variable as the mean relative phase headed towards 90º. This should sound familiar: it's the pattern of movement stability described by the HKB model!

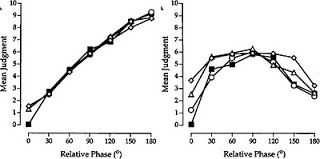Figure 1. Mean judgments of mean relative phase (left) and the standard deviation of those judgments (right). Adapted from Zaal et al, 2000.

Judgments of Phase Variability

Bingham et al also had participants make judgments of how coordinated the movement appeared (i.e. judgments of phase variability). The rationale was that, in the original Kelso experiments, participants were under a 'non-interference' instruction whereby they were told that if the coordination was too difficult to maintain, they were to allow themselves to transition into something easier. When moving at 180º and asked to speed up, the coordination does indeed become more variable prior to the transition to 0º, at which point variability drops again. The ability of participants to follow this instruction (and the fact of the transition itself) suggests that this variability is detected by the system.

Variability was added to the signals so that there was either 0º, 5º, 10º or 15º variability in the signal.

Mean variability was discriminated in the asymmetric inverted U-shaped function again; the four levels were only well discriminated at 0º and (at low frequencies) 180º. Elsewhere the levels became less reliably distinguished until they were indistinguishable at 90º; in addition, relative phases other than 0º and 180º were judged to be increasingly variable up to a maximum at 90º, even when there was no added variability.
The variability of the judgments of variability also followed the now familiar asymmetric inverted U-shaped function; not only could participants not discriminate the variability at 90º they were unreliable in what they did produce as a judgement.

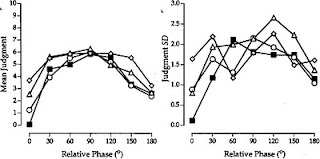Figure 2. Mean judgments of phase variability (left) and the standard deviation of those judgments (right). Adapted from Zaal et al, 2000.

In other words, in the absence of having to produce the movements themselves, participants making perceptual judgments produced a pattern of results that had the same qualitative form as the movement data. The implication is striking: coordinated movements are structured as described by the HKB model because of how we perceive them. The region around 0º is clearly discriminated and thus movements can be maintained there (small errors are quickly detected and corrected); the same is true at 180º, although less so and this gets worse with increases in frequency. Without training, 90º is never clearly perceived nor discriminated, and thus cannot be maintained.

Summary

The dynamic pattern approach had left us two unanswered questions: a prediction (is learning harder near stronger attractors; answer, no), and why does the HKB function end up in the shape that it does? The answer to this latter question now appears to be that 0º isn't easy because there's an attractor there; the HKB model ends up with an attractor there because 0º is easy, because it is readily perceived!

The scene is now set for a transition in our understanding of this task, from the dynamic pattern approach to a more complete perception-action approach. My next posts on coordination will therefore review the Bingham model and the empirical techniques we've developed along the way.

References

Bingham GP, Schmidt RC, & Zaal FT (1999). Visual perception of the relative phasing of human limb movements. Perception & psychophysics, 61 (2), 246-58 PMID: 10089759

Bingham, G., Zaal, F., Shull, J., & Collins, D. (2001). The effect of frequency on the visual perception of relative phase and phase variability of two oscillating objects Experimental Brain Research, 136 (4), 543-552 DOI: 10.1007/s002210000610

Fontaine, R. J., Lee, T. D., & Swinnen, S. P. (1997). Learning a new bimanual coordination pattern: Reciprocal influences of intrinsic and to-be-learned patterns. Canadian Journal of Experimental Psychology, 51(1), 1-9.

Schmidt, R. C., Carello, C., & Turvey, M. T. (1990). Phase transitions and critical fluctuations in the visual coordination of rhythmic movements between people. Journal of Experimental Psychology: Human Perception and Performance, 16(2), 227-247.

Wenderoth, N., Bock, O., & Krohn, R. (2002). Learning a new bimanual coordination pattern is influenced by existing attractors. Motor Control, 6, 166-182.

Zaal, F., Bingham, G., & Schmidt, R. (2000). Visual perception of mean relative phase and phase variability. Journal of Experimental Psychology: Human Perception and Performance, 26 (3), 1209-1220 DOI: 10.1037/0096-1523.26.3.1209

- A Perception/action Model Of Coordination
Other coordination posts are here. The role of perception in the dynamic leading to the HKB phenomena has been made clear by the work so far. But the exact form of this dynamic had yet to be modelled; the HKB model only consists of two cosine functions...

- Learning A Novel Coordination; Things Get Interesting
Other coordination posts are here. This will be a brief post to follow on from the last, in which I reviewed the early learning studies of Kelso & Zanone that led to the dynamic pattern hypothesis. These original studies looked comprehensive and compelling....

- Learning A Novel Coordination - The Dynamic Pattern Hypothesis
Other coordination posts are here. Recall this image:The HKB potential function, ~1HzThis basic layout is supposed to describe an intrinsic state of affairs, namely that only 0°and 180°are stable coordinations (+/- 180° are identical except for which...

- Coordination And The Haken-kelso-bunz Model
Other coordination posts are here. Now we have the basics out of the way, we can explore some of the key characteristics of coordinated rhythmic movements. Kelso's early experiments established a set of basic phenomena. Recall that, at the moment,...

- Coordinated Rhythmic Movement. - An Introduction To An Experimental Paradigm
I have some papers I wanted to talk about, but it occurred to me that they only make sense in a context. So I'm going to spend some time talking about the experimental task I use a lot, why it's interesting and what we can learn from it about...

Neuroscience