Neuroscience
- Visual Feedback For Training Novel Coordinations
The key feature of coordinated rhythmic movements is that not all coordinations are stable. Most other rhythms can be learned, however, which is why we can have jazz drumming. People have been training participants to perform novel coordinations (especially...
- Rates Of Learning And The Dynamic Pattern Approach
One of the interesting features of coordinated rhythmic movement is that people start out with a particular pattern to their performance - there is pre-existing structure to our attempts to coordinate these movements. This structure affects our ability...
- A Perception/action Model Of Coordination
Other coordination posts are here. The role of perception in the dynamic leading to the HKB phenomena has been made clear by the work so far. But the exact form of this dynamic had yet to be modelled; the HKB model only consists of two cosine functions...
- Visual Perception Of Coordinated Rhythmic Movements
Other coordination posts are here. Fontaine et al (1997) and Wenderoth et al (2002) had empirically established that a key prediction of the dynamic pattern hypothesis was false: learning was easier closer to 0° than it was to 180°. The HKB attractor...
- Coordination And The Haken-kelso-bunz Model
Other coordination posts are here. Now we have the basics out of the way, we can explore some of the key characteristics of coordinated rhythmic movements. Kelso's early experiments established a set of basic phenomena. Recall that, at the moment,...
Neuroscience
Learning a Novel Coordination - The Dynamic Pattern Hypothesis
Other coordination posts are here.
Recall this image:
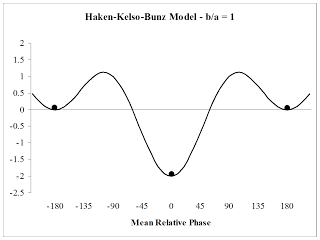 |
| The HKB potential function, ~1Hz |
This basic layout is supposed to describe an intrinsic state of affairs, namely that only 0°and 180°are stable coordinations (+/- 180° are identical except for which limb is lagging and which is leading). If you look at this function, you will see that potential energy is a maximum at +/90; this suggests that 90°is a maximally unstable coordination (i.e. it takes the most energy to maintain and is susceptible to perturbations which will make behaviour 'run off' towards one or other attractor). This is indeed the case, empirically; people can do it but fail to respond to the inevitable errors that accumulate and they lose the coordination very rapidly.
The question then is: can you learn to move at 90°? Is this dynamic pattern modifiable by experience?
If you're a drummer of any kind, you'll already know the answer: yes, but it's hard. The first people to look at learning were Pier Zanone and Scott Kelso, and they were interested in the consequences of learning across the space of possible coordinations. How is this dynamic modified by experience?
They developed a straight-forward methodology. First, they needed a feedback method, because people can't maintain 90° without help long enough to learn anything about it. They settled on the visual metronome, two displays of pairs of LEDs which flashed in the required pattern (e.g. the two top LEDs would light at the same time, and then the bottom two at the same time, to pace 0°). The participant's job was to match the flexion and extension of their fingers to these metronomes (one per finger) and thus reproduce the requested relative phase at a requested frequency.
This then enabled them to pace any given relative phase, which allowed them to a) train one relative phase (e.g. 90°) and then b) scan through all relative phases from 0° to 180° to see whether stability there had changed. These scans would provide them with a snapshot of the current actual shape of the potential function at various moments during training.
What they found was the following:
- Training at 90° seemed to 'drain' resources from the entire landscape, but especially from 180°. Movement stability there decreased during training but then recovered by the end.
- The effect of training at 90° was the creation of a third attractor centred there. Zanone & Kelso described this as a phase transition, a qualitative change in the underlying dynamics. They hypothesised that this phase transition required resources from the existing dynamic to be created, hence the temporary loss of stability at 180° while the system reorganised itself.
- This new-found ability to move at 90° only generalised to -90° (or 270°), the symmetry partner of the trained location that only differs in terms of which limb is leading or lagging. Zanone & Kelso took this to be evidence that what was being learned was an abstract control dynamic, not a specific pattern of limb movement.
They then tested some variants. For example, some participants come to the lab already able to do 90° - Zanone & Kelso trained these people to do, for example, 135° and scanned the resulting dynamic. This experiment revealed that the attractor at 90° moved to centre itself over 135°; three attractors seems to be the limit! They also tested their hypothesis about the abstract nature of the control dynamic being learned, by showing that learning a 90° phase relation between an arm and the opposite leg generalised to the other combination - this supported their hypothesis, that what was learned was an abstract control dynamic that could simply be plugged into any limb combination.
The Dynamic Pattern Hypothesis
These results lead to what has been the dominant theoretical approach to coordinated rhythmic movement, the dynamic pattern hypothesis. This approach claims the following:
- The HKB model describes the intrinsic dynamic of this task; this layout exists in the background and structures all attempts to produce a coordination. This structure in behaviour is a function of relative phase, which can thus be treated as an order parameter.
- 0° and 180° are attractors, i.e. preferred states of the system that draw other states towards them.0° is a stronger attractor than 180°.
- Learning these other states involves competing against these preferred states.
- PREDICTION: learning close to 0° will be harder than learning close to 180° because the stronger pull of 0° will interfere more with the process of learning.
- The result of learning is a new attractor; this qualitative change in the shape of the intrinsic dynamics is a phase transition.
Next time...
There remains a problem that this approach has failed to address: why is the intrinsic dynamic the shape that it is? And what happens when you test the prediction in 3.1?
- Visual Feedback For Training Novel Coordinations
The key feature of coordinated rhythmic movements is that not all coordinations are stable. Most other rhythms can be learned, however, which is why we can have jazz drumming. People have been training participants to perform novel coordinations (especially...
- Rates Of Learning And The Dynamic Pattern Approach
One of the interesting features of coordinated rhythmic movement is that people start out with a particular pattern to their performance - there is pre-existing structure to our attempts to coordinate these movements. This structure affects our ability...
- A Perception/action Model Of Coordination
Other coordination posts are here. The role of perception in the dynamic leading to the HKB phenomena has been made clear by the work so far. But the exact form of this dynamic had yet to be modelled; the HKB model only consists of two cosine functions...
- Visual Perception Of Coordinated Rhythmic Movements
Other coordination posts are here. Fontaine et al (1997) and Wenderoth et al (2002) had empirically established that a key prediction of the dynamic pattern hypothesis was false: learning was easier closer to 0° than it was to 180°. The HKB attractor...
- Coordination And The Haken-kelso-bunz Model
Other coordination posts are here. Now we have the basics out of the way, we can explore some of the key characteristics of coordinated rhythmic movements. Kelso's early experiments established a set of basic phenomena. Recall that, at the moment,...
